Baja tensión

Protección con interruptor automático en esquema TN-S

  • Publicado el
  • Actualizado el
IEBT. Ejercicios
1. Protección con interruptor automático en esquema TN-S
2. Cálculo de red subterránea
3. ¿Qué curva de disparo elijo para un motor?
4. Cálculo completo de instalación interior con agrupamiento de circuitos
5. Cálculo de la previsión de cargas de una LGA
6. Cálculo de la derivación individual de una vivienda, con propuesta de requisitos adicionales

En este ejercicio, se ilustra el cálculo básico de un circuito y también la comprobación de si un interruptor automático concreto es adecuado como protección ante contactos indirectos en un esquema de distribución de neutro TN-S.

Contenidos mostrar

Planteamiento

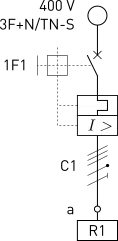
Ejercicio de comprobación de automático en esquema TN-S
Figura 1. Circuito de cálculo.

Considerando el circuito de la figura 1, los datos de los que se dispone son los siguientes:

  • 1F1, interruptor magnetotérmico: calibre I_n = 125\,\text{A}. Según su curva I vs t, la apertura en t = 0.4\,\text{s} ocurre para un valor de intensidad de 950 A.
  • C1, circuito:
    • Conductores unipolares, de Cu, aislados con PVC, sobre bandejas perforadas en recorrido horizontal.
    • Secciones para neutro y para CP con los mínimos valores posibles.
    • e = 0.5\%, L = 35\,\text{m}
  • R1, receptor sin factor de arranque: S = 70\,\text{kVA}, \cos\varphi = 0.9

Se desea calcular lo siguiente:

  1. Mínima sección para todos los conductores del circuito C1.
  2. Comprobar si 1F1 es adecuada como protección contra contactos indirectos.

Resolución propuesta

Mínima sección

Debe cumplir el criterio térmico y el de caída de tensión.

Caída de tensión

Se puede comenzar por cualquiera de los dos criterios, pero de entrada se observa en los datos de partida que el valor asignado como caída de tensión e es bastante restrictivo para la longitud del circuito. Es muy probable que este criterio sea el predominante para la sección final, por lo que se opta por comenzar el cálculo siguiendo este criterio. Los valores que se usarán en el cálculo son los siguientes:

    \begin{align*} P & = 70\cdot 10^{3}\cdot 0.9 = 63\cdot10^3\,\text{W}\\ Q & = 70\cdot 10^{3}\cdot \sin(\arccos 0.9) = 30.51\cdot10^3\,\text{var}\\ e &= \frac{0.5}{100}\cdot 400 = 2\,\text{V}\\ \sigma\Bigg|_{\text{Cu, 70 $^\circ$C}} &= 48.47\,(\Omega\text{mm}^2/\text{m})^{-1} \end{align*}

Utilizando la expresión para el cálculo de sección por caída de tensión, y teniendo en cuenta una reactancia para los conductores de valor X = 0.08\,\Omega/\text{km}, resulta el siguiente valor normalizado:

    \begin{align*} S_{CT} & = \frac{L\cdot P}{\sigma\cdot \left(U\cdot e - 10^{-3}\cdot \frac{X}{n}\cdot L\cdot Q\right)} = \\ & = \frac{35\cdot 63\cdot10^3}{48.47\cdot \left(400\cdot 2 - 10^{-3}\cdot \frac{0.08}{n}\cdot 35\cdot 30.51\cdot 10^3\right)} = \\ & = 63.66\,\text{mm}^2 \longrightarrow 70\,\text{mm}^2 \end{align*}

Sección por calentamiento

La intensidad de diseño del circuito es I_B = \frac{70\cdot10^3}{\sqrt{3}\cdot 400} = 101.03\,\text{A}. Se trata de conductores unipolares de cobre, aislamiento de PVC sobre bandeja perforada, lo que correspondería a método F según Norma UNE-HD 60364-5-52. Con la tabla para valores de intensidad a 40^\circ\text{C}, columna correspondiente a 3 conductores activos de PVC, resultaría que para una sección de 35 mm^2 la intensidad admisible es de 119 A \geq I_B.

Sección adoptada

La sección adoptada para los conductores de fase sería la mayor de ambas, por tanto 70 mm^2, cuya intensidad admisible es 185 A.

En este caso ya está preseleccionada la protección con un calibre de I_n = 125\,\text{A}, por lo que no es necesario hacer ninguna corrección de la sección ya que se verifican las condiciones necesarias de coordinación entre cable y protección.

La mínima sección de neutro se especifica en la ITC-BT-19, sección 2.2.2 (aunque en la tabla 1 de la ITC-BT-08 se permita un valor inferior), siendo igual a la sección de fase dado el valor resultante para las fases.

La mínima sección del conductor de protección se indica en la tabla 2 de la ITC-BT-18, siendo admisible utilizar la mitad que la sección de fase. Por tanto, S_{CP} = 35\,\text{mm}^2.

En resumen, el circuito C1 sería de la siguiente forma:

4 x H07V-K 1X70 + H07V-K 1G35

Comprobación de la protección ante contactos indirectos

Se trata de un esquema de distribución TN-S. Esto significa que se distribuye el conductor de protección desde la alimentación. Por tanto, cuando se produce un defecto de aislamiento (y con ello la posibilidad de un contacto indirecto), ocurre un cortocircuito fase-conductor de protección.

Para verificar si la protección es adecuada, debe comprobarse que ese hipotético cortocircuito de lugar a una intensidad lo suficientemente elevada como para activar el disparo del interruptor magnetotérmico. Este valor de intensidad con el que realizar la comprobación debe ser el más desfavorable posible, es decir, el valor mínimo de la intensidad de cortocircuito.

Según la ITC-BT-24 y la Norma UNE-HD 60364-4-41, el interruptor automático debe cumplir:

(1)   \begin{equation*} Z_s\cdot I_a \leq U_0 \end{equation*}

siendo,

  • Z_s: impedancia del bucle de defecto. En este caso tendríamos en cuenta la impedancia que presenta el circuito C1. Lo que pretendemos verificar es si el interruptor automático sería capaz de detectar el peor defecto de aislamiento posible. Esto ocurriría con la mínima intensidad de cortocircuito fase-conductor de protección. Por tanto, buscamos analizar el bucle con la máxima impedancia, lo que se daría a la máxima temperatura posible de los conductores elegidos para la situación de cortocircuito (160^\circC en el caso del PVC). La resistividad del cobre a esa temperatura es de 0.0267\,\Omega\text{mm}^2/\text{m}.
  • I_a: intensidad que asegura el funcionamiento del interruptor automático en un tiempo máximo indicado. La tabla 1 de la ITC-BT-24 (tabla 41.1 de UNE-HD 60364-4-41) no sería de aplicación en este caso porque la intensidad del circuito no entra dentro de los requisitos de aplicación de dicha tabla. En ella se indica que el tiempo de disparo debería ser como máximo de 0,4 s para una tensión del bucle de defecto de 230 V. La Norma citada admite que el tiempo máximo de desconexión fuera de 5 s en una situación como esta. No obstante, es más prudente realizar la comprobación para el tiempo de 0,4 s especificado para el resto de situaciones.
  • U_0: valor eficaz de tensión entre fase y el conductor de protección, para corriente alterna. En esta instalación sería 230 V.

Según lo explicado para la impedancia del bucle de defecto, y teniendo en cuenta que lo forma la impedancia de una fase y la del conductor de protección, el valor más desfavorable para este cálculo sería:

    \begin{align*} Z_s & =\sqrt{ \left( R_{\text{fase}} + R_{\text{CP}} \right)^2 + \left( X_{\text{fase}} + X_{\text{CP}} \right)^2 } =\\ & = \sqrt{ \left( \rho_{\text{max}}\cdot\frac{L_{\text{fase}} }{S_{\text{fase}} } + \rho_{\text{max}}\cdot\frac{L_{\text{CP}} }{S_{\text{CP}} } \right)^2 + \left( X_{\text{fase}} + X_{\text{CP}} \right)^2 } =\\ & = \sqrt{ \left( 0.0267 \cdot\frac{35 }{70 } + 0.0267 \cdot\frac{35 }{35 } \right)^2 + \left( 0.08\cdot 0.035 + 0.08\cdot 0.035 \right)^2 } = \\ & = 0.0404\,\Omega \end{align*}

donde se han despreciado las impedancias de motores, de transformador y de red, según la recomendación de UNE-EN 60909-0. El análisis que podríamos hacer llegados a este punto es el siguiente:

  • La intensidad a la que debería producirse el corte en 0,4 s se obtiene de la expresión (1) y debería valer:

    \[ I_a \leq \frac{230}{0.0404} = 5\,693\,\text{A} \]

  • La mínima intensidad de cortocircuito posible, provocada en el extremo final del circuito C1 (punto a de la figura 1) y calculada según las recomendaciones de la Guía de Interpretación del REBT (anexo 3), valdría:

    \[ I_{cc\text{,min}} = \frac{0.8\cdot 230}{0.0404} = 4\,554.46\,\text{A} \]

El valor estimado para el cortocircuito es la situación más desfavorable que nos podemos llegar a encontrar respecto a la posibilidad de que no fuera suficientemente elevada para provocar la actuación del interruptor automático en el tiempo máximo deseado. Por ese motivo, este valor es el que deberíamos usar para comparar si verifica el resto de condiciones.

  1. Por un lado, I_a [t=0.4\,\text{s}] = 950\,\text{A} \leq 5\,693\,\text{A} y se cumpliría esta condición.
  2. Por otro lado, hemos comprobado que la intensidad que se tendría en el caso de producirse el defecto, efectivamente resultaría de un valor comprendido en el rango de disparo deseado: I_{cc\text{,min}} = 4\,554.46\,\text{A} \geq 950\,\text{A}

Por tanto, sería válido como protección ante contacto indirecto en este esquema.

 

Compártelo:

Narciso Moreno-Alfonso
Profesor Titular en el Departamento de Ingeniería Eléctrica de la Universidad de Sevilla. Mi formación universitaria es de Ingeniero Técnico Industrial en Electricidad, Ingeniero en Electrónica y Diploma de Estudios Avanzados en Electrónica de Potencia (Energías Renovables). Mis áreas de trabajo e investigación son: instalaciones eléctricas, energías renovables, Big Data.

Artículos relacionados

29/11/2023

Aparamenta de protección. Datos de magnetotérmicos

14/11/2023

Aparamenta eléctrica

13/11/2023

Verificación de instalaciones eléctricas. Parte I

09/11/2023

Cálculo de red subterránea

09/10/2023

Introducción a las instalaciones eléctricas de baja tensión

Ver más

Comentarios

Esta entrada tiene 0 comentarios

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *